समकोण त्रिभुज (परिभाषा, क्षेत्रफल, सूत्र, परिमाप, गुण और उदाहरण)

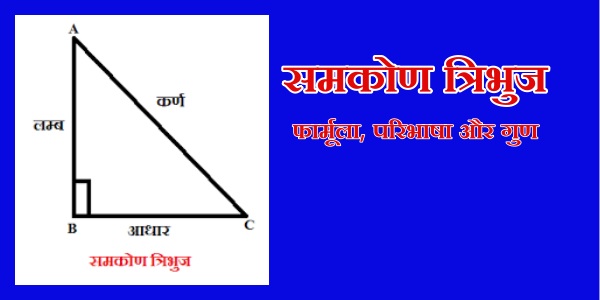
Samkon Tribhuj: गणित में विभिन्न प्रकार के बहुभुज आकार होते है, इनमें से एक बहुभुज आकार त्रिभुज है। त्रिभुज के विभिन्न प्रकार होते हैं, उनमें से एक प्रचलित प्रकार समकोण त्रिभुज का है। सरल शब्दों में कहें तो एक ऐसा त्रिभुज जो 90 डिग्री का कोण बनाता हो।

इस तरह के त्रिभुज से जुड़े विभिन्न प्रकार के प्रश्न आपके समक्ष गणित में आएंगे, जिन्हें हल करने के लिए आपको समकोण त्रिभुज का क्षेत्रफल, फार्मूला परिमाप, परिभाषा गुण और उदाहरण के बारे में विस्तार पूर्वक जानकारी होनी चाहिए।

अगर आज समकोण त्रिभुज (Samkon Tribhuj) के बारे में इस तरह की जानकारी ढूंढ रहे हैं तो आज के लेख में हम आपको समकोण त्रिभुज के संबंध में विस्तार पूर्वक जानकारी दिए हैं, उन सभी बातों को ध्यान पूर्वक नीचे पढ़ें।

समकोण त्रिभुज (परिभाषा, क्षेत्रफल, सूत्र, परिमाप, गुण और उदाहरण) | Samkon Tribhuj

विषय सूची

समकोण त्रिभुज की परिभाषा

किसी भी चीज को समझने से पहले आपको उसकी परिभाषा के बारे में विस्तारपूर्वक जानकारी होनी चाहिए। इस संबंध में अगर आपको बताए तो समकोण त्रिभुज एक ऐसा बहुभुज आकार होता है, जो तीन रेखाओं को बंद करने से बनता है। यह आकृति इस प्रकार बंद होती है कि आकृति के अंदर दो रेखाओं के मिलने पर 90 डिग्री का कोण बनता है।

सरल शब्दों में कहें तो तीन रेखा से बना एक ऐसा बंदा आकार जिसके अंदर एक 90 डिग्री का कोण बना हो, उसे समकोण त्रिभुज कहेंगे। इस तरह के कोण में तीन प्रकार की भुजाएं होती हैं एक भुजा जो ऊपर से नीचे की ओर आती है, वह आधार पर मौजूद भुजा का लंबवत होती है।

इस तरह के आखिरी दिन में दो भुजाओं के स्क्वायर का योग हमेशा तीसरी भुजा के स्क्वायर के बराबर होता है या हम यूं कह सकते हैं कि एक भुजा का आकार बड़ा और बाकी का दो उससे छोटा होता है।

समकोण त्रिभुज के गुणधर्म

किसी भी आकृति को विस्तार पूर्वक समझने के लिए उसके गुण धर्म की समझ होना आवश्यक है। इस वजह से इस आकृति के क्या गुण धर्म है, इसके बारे में नीचे कुछ बातें बताई गई है।

समकोण त्रिभुज में एक एंगल 90 डिग्री का होता है।
समकोण त्रिभुज की एक भुजा बाकी दोनों भुजाओं से अधिक लंबी होती है। साथ ही दो भुजाओं के स्क्वायर का योग तीसरी भुजा के स्क्वायर के बराबर होता है।
आयत अन्य वर्ग को उसके कारण से विभाजित करते हैं तो हमें दो समकोण त्रिभुज मिलते हैं।
किसी समकोण त्रिभुज में जो दो एंगल होती हैं, उनका योग 90 डिग्री होता है।

यह भी पढ़े: त्रिभुज किसे कहते हैं?, प्रकार, क्षेत्रफल एवं सूत्र

समकोण त्रिभुज के प्रकार

आपको बता दें कि समकोण त्रिभुज के कुछ प्रकार होते है:

समबाहु समकोण त्रिभुज
विषमबाहु समकोण त्रिभुज

समबाहु समकोण त्रिभुज

या ऐसे त्रिभुज होते है, जिनकी दो भुजाएं बराबर होते है और दूकान भी बराबर होते है अर्थात आपको इस तरह के त्रिभुज में एंगल के मान 45, 45 और एक 90 डिग्री का मिलेगा। इसके अलावा इस त्रिभुज में आधार और ऊंचाई का मान एक समान होती है।

अर्थात जब कोई आपको ऐसा त्रिभुज मिले, जिसमें एक एंगल 90 हो और बाकी के दो एंगल एक समान हो और दो भुजाएं भी एक समान हो तो इस तरह के त्रिभुज को समबाहु समकोण त्रिभुज कहते हैं।

विषमबाहु समकोण त्रिभुज

यह एक खास किस्म का त्रिभुज होता है, जिसमें किसी भी प्रकार की भुजाएं एक समान नहीं होते हैं तीनों भुजाएं हैं अलग-अलग मान की होती है। साथ ही इस तरह के त्रिभुज में एक एंगल 90 और बाकी के दो अलग-अलग मान के होते हैं।

मगर आपको बता दें चाहे आप किसी भी प्रकार के समबाहु त्रिभुज की बात कर रहे हो, उसका क्षेत्रफल और परिमाप का सूत्र एक समान ही होता है, उसमें किसी भी प्रकार का परिवर्तन नहीं होता।

समकोण त्रिभुज का क्षेत्रफल (samkon tribhuj ka kshetrafal)

जब आकृति की परिभाषा और गुणधर्म की समझ हो गई है तो इस आकृति से जुड़े प्रश्न को हल करने के लिए आपको यह मालूम होना चाहिए कि यह आकृति कितना जगह छेक रही है। इसके लिए समकोण त्रिभुज का क्षेत्रफल ज्ञात करना आवश्यक है, जिस से जुड़े सूत्र नीचे दिए गए है। समकोण त्रिभुज के क्षेत्रफल का अर्थ होता है कि समकोण त्रिभुज कितना जगह छेक रही है।

क्षेत्रफल = A = ½ × b × h अर्थात, A = ½ × आधार × ऊँचाई।

याद रखें कि समकोण त्रिभुज में जिन दो रेखाओं के मिलने से 90 डिग्री का कौन बन रहा है, उन्हीं दोनों रेखा में से किसी एक को आधार और किसी एक को ऊंचाई मान ली जाती है।

क्षेत्रफल A =√ [ s(s – a)(s – b)(s – c) ]

यहां s का तात्पर्य अर्थ परिधि से है जिसका मान = a+b+c /2 होता है। इस सूत्र से आप किसी भी प्रकार के त्रिभुज क्षेत्रफल का मान बड़ी आसानी से निकाल सकते हैं।

समकोण त्रिभुज का परिमाप (samkon tribhuj ka parimap)

किसी भी आकृति के परिमाप का अर्थ होता है, उस आकृति के बाहरी बॉर्डर कितने लंबे है। जब हम किसी चीज के बाहरी लंबाई को नाप लेंगे तो उससे परिमाप कहेंगे। अगर हम समकोण त्रिभुज के परिमाप की बात करें तो उसका एक सूत्र होता है।

समकोण त्रिभुज का सूत्र – a+b+c, अर्थात समकोण त्रिभुज के तीनो भुजाओं का योग ही उसका परिमाप होता है।

FAQ

समकोण त्रिभुज किसे कहते हैं?

समकोण त्रिभुज एक ऐसा त्रिभुज होता है, जिसमें तीन भुजाएं हैं एक बंदा आकार बनाती है और उस बंद आकार के अंदर एक 90 डिग्री का कोण होता है।

समकोण त्रिभुज का क्षेत्रफल क्या होता है?

समकोण त्रिभुज का क्षेत्रफल = A = ½ × b × h अर्थात, A = ½ × आधार × ऊँचाई होता है।

कोई ऐसा सूत्र जिससे हम किसी भी प्रकार के त्रिभुज का मान निकाल सके?

हर त्रिभुज के क्षेत्रफल को ज्ञात करने के लिए अलग-अलग प्रकार के सूत्र होते हैं। मगर केवल एक सूत्र ऐसा है, जिसका इस्तेमाल करके आप किसी भी त्रिभुज के क्षेत्रफल का मान बड़ी आसानी से निकाल सकते है = A =√ [ s(s – a)(s – b)(s – c) ] यहां s का तात्पर्य अर्थ परिधि से है, जिसका मान = a+b+c /2 होता है। इस सूत्र से आप किसी भी प्रकार के त्रिभुज क्षेत्रफल का मान बड़ी आसानी से निकाल सकते हैं।

निष्कर्ष

हमने अपने आज के इस महत्वपूर्ण लेख में आप सभी लोगों को समकोण त्रिभुज का क्षेत्रफल, फार्मूला परिमाप, परिभाषा एवं उदाहरण? के बारे में पूरी विस्तार पूर्वक जानकारी प्रदान की हुई है और साथ ही हमने साधारण शब्दों में आपको इस लेख से संबंधित जानकारी दी हुई है।

अगर आपके मन में हमारे आज के इस लेख से संबंधित कोई भी सवाल या फिर कोई भी सुझाव है तो आप हमें कमेंट बॉक्स में बता सकते है। हम आपके द्वारा दिए गए प्रतिक्रिया का जवाब शीघ्र से शीघ्र देने का पूरा प्रयास करेंगे और हमारे इस महत्वपूर्ण लेख को अंतिम तक पढ़ने के लिए आपका बहुत-बहुत धन्यवाद एवं आपका कीमती समय शुभ हो।

यह भी पढ़े

रेखाएँ किसे कहते हैं?, परिभाषा, प्रकार और उदाहरण

समबाहु त्रिभुज (फार्मूला, परिभाषा और गुण)

वृत्त (परिभाषा, क्षेत्रफल, परिधि, त्रिज्या, व्यास, जीवा, परिमाप)

बेलन किसे कहते है? (भेद, गुणधर्म, सूत्र, आयतन एवं उदाहरण)