Cube Root Table: जब आप गणित के विषय में खुद को और भी तेज बनाना चाहते है और सभी गणित के प्रश्नों को चुटकियों में हल करना चाहते हैं तो इसमें आपकी सहायता वर्ग और घन कर सकते है। यदि आपको कम से कम ५० तक के वर्ग और घन याद है तो आप कोई भी गणितीय गणना जल्दी से हल कर सकते हैं।
गणितीय गणनाओं को जल्दी से हल करने के लिए हम आपके लिए यहाँ 1 से 100 तक घनमूल सारणी लेकर हैं, जो आपको किसी भी तरह की गतितीय गणना, प्रश्न और जोड़-हिसाब में मदद करेगी।
आपको तो पता ही होगा घनमूल सारणी पूरा कंठस्थ याद हो तो आपकी गणितीय गणना या कैलकुलेशन करना बहुत ही सरल हो जाता है।
यह भी पढ़े: 1 से 100 तक वर्ग और वर्गमूल सारणी
1 से 100 तक घनमूल सारणी | Cube Table 1 To 100 | घनमूल सारणी | Cube Root Table
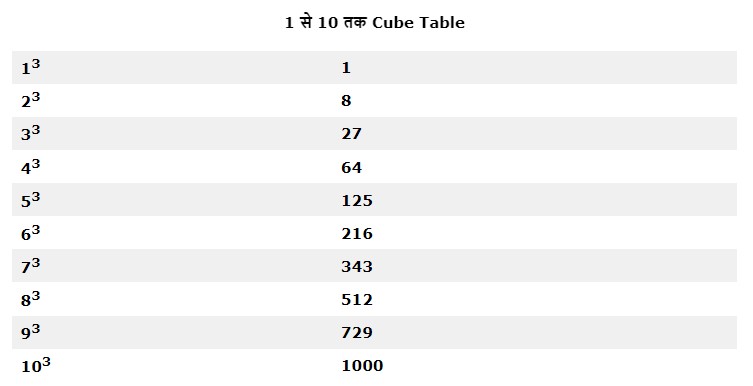
1 से 10 तक घनमूल
| 13 | 1 |
| 23 | 8 |
| 33 | 27 |
| 43 | 64 |
| 53 | 125 |
| 63 | 216 |
| 73 | 343 |
| 83 | 512 |
| 93 | 729 |
| 103 | 1000 |
11 से 20 तक घनमूल
| 113 | 1331 |
| 123 | 1728 |
| 133 | 2197 |
| 143 | 2744 |
| 153 | 3375 |
| 163 | 4096 |
| 173 | 4913 |
| 183= | 5832 |
| 193 | 6859 |
| 203 | 8000 |
21 से 30 तक घनमूल
| 213 | 9261 |
| 223 | 10648 |
| 233 | 12167 |
| 243 | 13824 |
| 253 | 15625 |
| 263 | 17576 |
| 273 | 19683 |
| 283 | 21952 |
| 293 | 24389 |
| 303 | 27000 |
31 से 40 तक घनमूल
| 313 | 29791 |
| 323 | 32768 |
| 333 | 35937 |
| 343 | 39304 |
| 353 | 42875 |
| 363 | 46656 |
| 373 | 50650 |
| 383 | 54872 |
| 393 | 59319 |
| 403 | 64000 |
41 से 50 तक घनमूल
| 413 | 68921 |
| 423 | 74088 |
| 433 | 79507 |
| 443 | 85184 |
| 453 | 91125 |
| 463 | 97336 |
| 473 | 103823 |
| 483 | 110592 |
| 493 | 117649 |
| 503 | 125000 |
51 से 60 तक घनमूल
| 513 | 132651 |
| 523 | 140608 |
| 533 | 148877 |
| 543 | 157464 |
| 553 | 166375 |
| 563 | 175616 |
| 573 | 185193 |
| 583 | 195112 |
| 593 | 205379 |
| 603 | 216000 |
61 से 70 तक घनमूल
| 613 | 226981 |
| 623 | 238328 |
| 633 | 250047 |
| 643 | 262144 |
| 653 | 274625 |
| 663 | 287496 |
| 673 | 300763 |
| 683 | 314432 |
| 693 | 328509 |
| 703 | 343000 |
71 से 80 तक घनमूल
| 713 | 358911 |
| 723 | 373248 |
| 733 | 389017 |
| 743 | 405224 |
| 753 | 421875 |
| 763 | 438976 |
| 773 | 456533 |
| 783 | 474552 |
| 893 | 493039 |
| 803 | 521000 |
81 से 90 तक घनमूल
| 813 | 531441 |
| 823 | 551368 |
| 833 | 571787 |
| 843 | 592704 |
| 853 | 614125 |
| 863 | 636056 |
| 873 | 658503 |
| 883 | 681472 |
| 893 | 704969 |
| 903 | 729000 |
91 से 100 तक घनमूल
| 913 | 753571 |
| 923 | 778688 |
| 933 | 804357 |
| 943 | 830584 |
| 953 | 857375 |
| 963 | 884736 |
| 973 | 912673 |
| 983 | 941192 |
| 993 | 970299 |
| 1003 | 1000000 |
Cube Root Table 1-100 PDF Download
हमने यहाँ पर घनमूल सारणी को पीडीऍफ़ रूप में उपलब्ध किया है। आप इसे आसानी से डाउनलोड करके अपने प्रोजेक्ट आदि में प्रयोग में ले सकते है।
अपने इस लेख में सीखा कि घनमूल क्या होता है और 1 से 100 तक घनमूल सारणी कैसे बनाई जाती है। आपको इसे याद रखना होगा। यदि आप इस घनमूल सारणी में कंठस्थ रखते है तभी आप अपनी गणितीय गणना को आराम से और जल्दी से हल कर पाएंगे।
यह भी पढ़े
घन (क्षेत्रफल, परिमाप, आयतन, गुणधर्म, परिभाषा)
त्रिभुज किसे कहते हैं?, प्रकार, क्षेत्रफल एवं सूत्र
रेखाएँ किसे कहते हैं?, परिभाषा, प्रकार और उदाहरण