Ghan Kise Kahate Hain: घन एक त्रिविमीय ज्यामिति आकार है, जिसमें छह फलक और 12 किनारे होते है। हम अपने जीवन में जितनी भी चीजों को देखते हैं, वह 3 डाइमेंशनल या त्रिविमीय होती है। इस वजह से हमें इस तरह के आकार के बारे में जानने की आवश्यकता है।
हम अपने रोजमर्रा के जीवन में जितनी भी तस्वीरें देखते हैं, वह त्रिविमीय होती हैं। इस वजह से हमें इस तरह के आकार के बारे में जानकारी लेने की आवश्यकता है।
यहाँ पर घन के क्षेत्रफल, परिमाप, आयतन, गुणधर्म, परिभाषा के बारे में विस्तारपूर्वक जानकारी देने जा रहे है, जिसका इस्तेमाल करके आप विभिन्न परीक्षाओं के गणित छेत्र में अच्छा अंक हासिल कर सकते हैं।
घन किसे कहते हैं? (क्षेत्रफल, परिमाप, आयतन, गुणधर्म) | Ghan Kise Kahate Hain
घन की परिभाषा (Ghan Ki Paribhasha)
घन वर्ग की तरह दिखाई देगा। आप ऐसा समझ सकते है कि 6 वर्ग जब एक साथ जुड़ जाते हैं तो वह घन बन जाते है। सरल और सटीक तरीके से इसकी परिभाषा की बात करें तो एक ऐसी त्रिविमीय आकृति जिसमें 6 फलक, 12 किनारे और 8 कोने होते है, उसे हम घन कहते है।
घन की सभी भुजाएं एक समान होती है, जिस वजह से जब हम खान को एक दिशा से देखते हैं तो वह एक वर्ग की तरह दिखता है। मगर चारों ओर से देखने पर यह बहुत सारे घन का मिश्रण नजर आता है।
घन का चित्र (Ghan Ka Chitra)
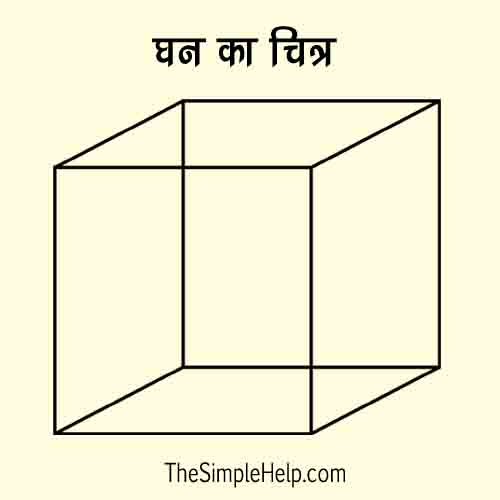
घन का गुणधर्म
घन एक आकृति है, जिसके कुछ खास गुण होते हैं। जिनके बारे में आपको पता होना चाहिए ताकि आप इस आकृति से जुड़े गणितीय सवालों को हल कर सके।
- घन की सभी भुजाएं बराबर होती है, इस वजह से एक घन की ऊंचाई, लंबाई और चौड़ाई एक समान होती है।
- घन के तीन फलक होते है, जिस वजह से इस आकृति में आप एंगल नहीं माप सकते। मगर एक घर में 6 वर्ग होते हैं, इस वजह से हर एक वर्ग की अगर बात की जाए तो उसमें वर्ग के गुणधर्म लगते हैं।
- घन वर्ग का त्रिविमीय आकार है, इस वजह से इसमें लंबाई, ऊंचाई और चौड़ाई के संबंधित चीजों पर चर्चा की जाती है। इसमें एंगल पर चर्चा नहीं की जाती।
- घन की भुजा की लंबाई को अगर X गुना बढ़ा दिया जाए तो उसका क्षेत्रफल X2 गुना बढ़ जाता है। साथ ही आयतन X3 गुना बढ़ जाता है।
- घन का सभी किनारा एक समान होता है। आयतन से घन के किनारे की लंबाई पता करने का फार्मूला 3√आयतन होता है।
घन का परिमाप
जैसा कि आपको पता होगा किसी भी आकृति का परिमाप उसके सभी भुजाओं का योग होता है। एक घन को जब आप ध्यान पूर्वक देखेंगे तो यह पाएंगे कि उसमें 12 भुजाएं होती हैं। अर्थात जब आप उन सभी भुजाओं का योग करेंगे तो आपको घन का परिमाप मिल जाएगा। मगर घन की सभी भुजाएं बराबर होती है, इस वजह से इसका एक सरल सूत्र बनाया गया है।
घन का परिमाप = 12 X a (जहाँ a घन की भुजा को दर्शाता है)
घन का क्षेत्रफल
क्षेत्रफल का अर्थ होता है कि किसी आकृति के द्वारा कितनी जगह ली जा रही है। जैसा कि हम जानते हैं घन में छह फलक होते हैं, जो वर्ग के आकार के होते हैं। जब हम किसी गाने को किसी जगह पर रखते हैं तो वह अपने एक वर्गीय फलक से उस जगह को घेरता है।
मगर जब हम इसी घन को किसी त्रिविमीय जगह पर रखेंगे तो वह अपने सभी फलक से जगह घेरेगा और इस वजह से हम यह कह सकते है कि एक फलक के द्वारा घेरी जा रही जगह को अगर 6 से गुणा कर दिया जाए तो उस घन के द्वारा जितना जगह है घेरा जा रहा है, उसकी संपूर्ण जानकारी मिल जाएगी।
जैसा कि हम जानते हैं एक वर्ग के द्वारा घेरी जा रही जगह या क्षेत्रफल का सूत्र भुजा गुना भुजा होता है। उसी प्रकार एक गाने में 6 वर्ग आते हैं, जो किसी त्रिविमीय स्थान पर जगह घेरते हैं।
घन का क्षेत्रफल = 6 (भुजा X भुजा)
= 6 (भुजा)2
घन से दो प्रकार का क्षेत्रफल निकलता है
जब आप घन के संबंध में कोई गणितीय सवाल हल करेंगे तो आप से दो किस्म के पृष्ठीय क्षेत्रफल के बारे में पूछा जाएगा।
घन का संपूर्ण क्षेत्रफल
जैसा कि हमने आपको बताया जब एक घन को किसी त्रिविमीय जगह पर रखेंगे तो वह सभी दिशाओं से जगह घेरेगा, जिस वजह से संपूर्ण पृष्ठीय क्षेत्रफल वर्ग के द्वारा घेरे जाने वाली जगह का 6 गुना होगा।
घन का संपूर्ण पृष्ठीय क्षेत्रफल = 6 X (भुजा X भुजा)
घन का पार्श्व पृष्ठीय क्षेत्रफल
कुछ सवाल ऐसे भी पूछे जाएंगे जब घन का केवल पार्थिव पृष्ठ का क्षेत्रफल पूछा जाएगा। अर्थात घन के निचले वर्ग और ऊपर के वर्ग को छोड़कर चारों दिशाओं में जो वर्ग हैं केवल उन चारों का क्षेत्रफल।
घन का पार्श्व पृष्ठीय क्षेत्रफल = 4 X (भुजा X भुजा)
घन का आयतन
आयतन का अर्थ होता है कि वह अपने अंदर कितना क्षेत्रफल रखा है। अर्थात अगर आप कोई चीज है घन में भरना चाहते हैं तो कितना भर सकते हैं, इसका सटीक माप आयतन से पता चलता है।
किसी भी वस्तु का आयतन उसके लंबाई, चौड़ाई और ऊंचाई को गुणा करने से पता चलता है।
घन का आयतन = लंबाई X चौड़ाई X ऊंचाई = (भुजा)3
घन के विकर्ण की लंबाई
जब हम किसी घन के कोने से कोने को मिलाने का प्रयास करते हैं तो कितनी दूरी होती है। अर्थात घन के एक ऊपरी कोने से उसके तिरछे निचली कोने तक की दूरी कितनी होती है, उसे हम विकर्ण की दूरी कहते हैं।
घन के विकर्ण की दूरी = √(3 X भुजा)
घन के भुजा की लंबाई
अब तक आपने देखा होगा कि सभी सूत्र में भुजा के बारे में पता होना आवश्यक है। मगर जब आपको भुजा की जानकारी ना हो तो घन की भुजा की लंबाई किस प्रकार पता करते है इसके लिए सूत्र –
भुजा = √(क्षेत्रफल / 6)
ऊपर दिए गए सभी प्रकार के सूत्र को अगर आप याद रखते हैं तो घन के संबंध में आपसे किसी भी प्रकार का प्रश्न पूछा जाए तो आप उसे बखूबी हल कर लेंगे।
FAQ
एक ऐसा त्रिविमीय आकार जिसमें 6 फलक, 12 किनारे और आठ कोने होते है। साथ ही इस आकार की सभी भुजाएं एक समान होती है।
आपको यह बात याद रखना चाहिए कि एक घन का सभी भुजा का मान एक समान होता है। इस वजह से जब हम घन की भुजा को दुगना करते है तो इसका क्षेत्रफल 4 गुना बढ़ जाता है और उसका आयतन 8 गुना बढ़ जाता है।
भुजा X भुजा X भुजा घन के आयतन का सूत्र होता है।
घन के विकर्ण की लंबाई = घन के विकर्ण की दूरी = √(3 X भुजा)
निष्कर्ष
हमने यहाँ पर के घन किसे कहते हैं?, क्षेत्रफल, परिमाप, आयतन, गुणधर्म (Ghan Kise Kahate Hain) बारे में जानकारी शेयर की है। उम्मीद करते हैं आपको यह लेख पसंद आया होगा, इसे आगे शेयर जरूर करें। यदि आपका इस लेख से जुड़ा कोई सवाल या सुझाव है तो कमेंट बॉक्स में जरूर बताएं।